
‘What stuff do you want your students to know, understand and be able to do if you have taught them a rich, challenging subject curriculum?’ This question is at the root of all our conversations in our new book Huh.
I got a grade A at A Level mathematics nearly 40 years ago. Since I have been a teacher (and especially since I have been a headteacher at Huntington) I have dabbled in teaching mathematics, made overly confident by my A Level grade.
My ability at mathematics was certainly strengthened by my strong metacognitive processes which made me resilient when solving equations. But there is so much I do not understand about mathematics. I never understood whole swathes of what we did in mathematics lessons, I just knew how to perform certain procedures to solve problems. For instance, I know that 32x2 differentiated equals 64x but I have no flying clue why. It makes me dangerous teaching mathematics, because all I can do is teach students how to jump through hoops. If one of them put their hand up and asked, “Sir, why does 32x2 differentiated equals 64x?” I couldn’t answer them.
I once watched in awe as Matt Smith, Huntington’s Deputy Headteacher, now acting Headteacher, taught a Further Maths Year 11 GCSE class. He used the unit circle (where the radius of the circle is 1) to show how to derive two important trigonometry identities: sin(x)/cos(x)=tan(x), and sin2(x) + cos2(x) = 1.
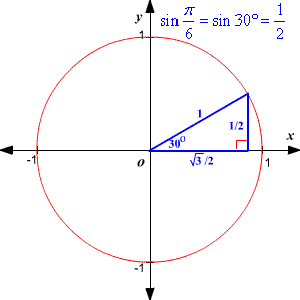
If we work in centimetres, the unit circle has a radius of 1 cm. Therefore the Sin 30 = Opposite/Hypotenuse = 0.5/1 = 0.5 cm.
He then showed us that for an angle of 30 degrees in a right angled triangle, the ratio of Opposite/Hypotenuse (AKA Sine) is always 0.5 no matter the lengths of the sides of the right angled triangle:
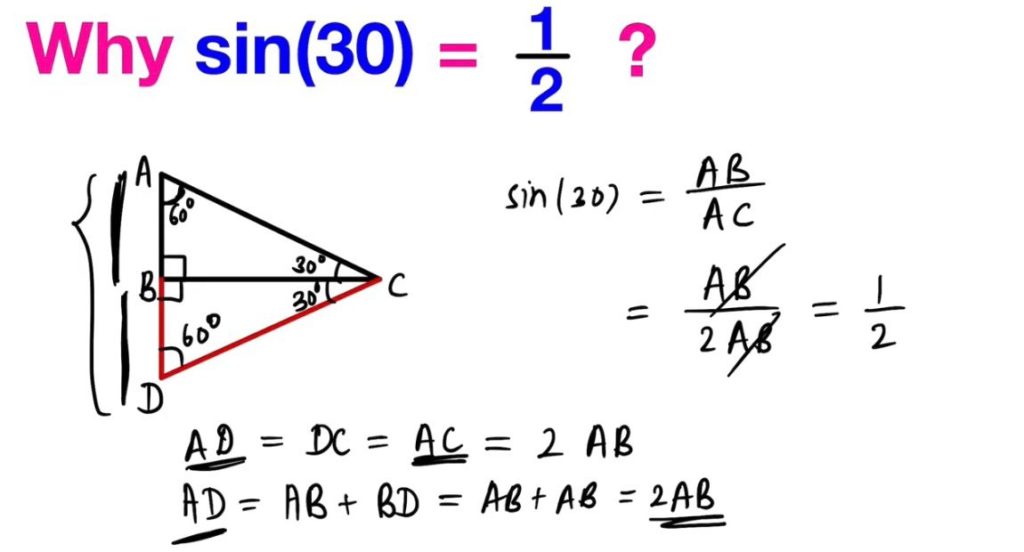
I was sitting at the back of the class as Matt delivered his crystal clear explanation. I yelped for joy and then had to explain to the class that for several decades I had known that Sin 30 was 0.5, but until Mr Smith had explained it, I had not understood why it was 0.5. They looked at me sympathetically, beneficiaries of having been taught by Matt, someone who understood mathematics.
Matt sent me a few notes, below, to help with this blog post.
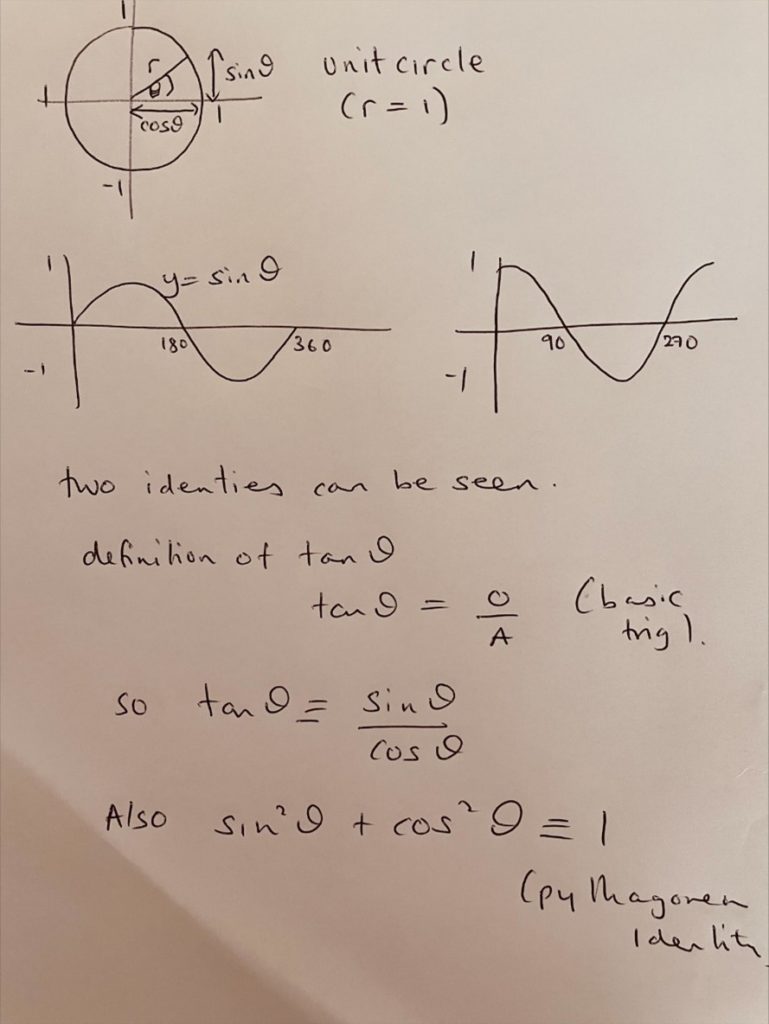
My point is that you cannot teach something so that students know and understand it, if you do not know and understand it yourself. No matter how good your pedagogy, if you do not understand the content of what you are teaching you are going to struggle.
Between March and June this year, Mary Myatt and I interviewed over 20 subject leaders about curriculum development. You can watch our interviews for free on Mary’s video channel, Myatt and Co., here. In Huh, where the essence of those interviews has been transcribed, you will find subject leaders explaining the very essence of their subject, how they structure the curriculum for understanding, how they prioritise education over examination hoop-jumping and how they support their colleagues with improving their own subject knowledge and understanding.
The subject leaders have been incredibly generous. Working with Mary has been a blast. It has been exhilarating, revelatory work, as exciting as that moment a few years ago when sitting in Matt Smith’s lesson, for the first time I began to understand mathematics for real…
(PS – catch Mary and me talking about Huh at the national researchED conference on Saturday 4 September 2021 in London – get your tickets here: https://researched.org.uk/event/researched-national-conference-2021/)
